Floating Point Round Off Error In Raptor Applications: Difference between revisions
| (9 intermediate revisions by 2 users not shown) | |||
| Line 9: | Line 9: | ||
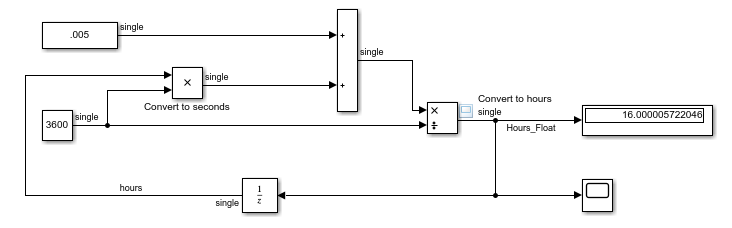
The customer was attempting to create an hour accumulator that would update during a 5 ms task. The customer wanted to view the value in hours in Raptor-Cal. This is a simplified version of their subsystem: | The customer was attempting to create an hour accumulator that would update during a 5 ms task. The customer wanted to view the value in hours in Raptor-Cal. This is a simplified version of their subsystem: | ||
[ | [[File:Fproundoff example float mult accumulators.png]] | ||
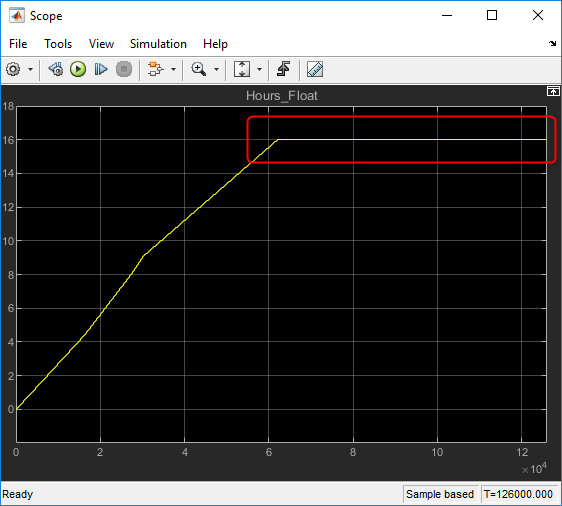
To investigate, simulation is easier to use than running on the controller. The simulation results shows the saturation at 16 hours that the customer claimed: | To investigate, simulation is easier to use than running on the controller. The simulation results shows the saturation at 16 hours that the customer claimed: | ||
[ | [[File:Saturation 16hours.png]] | ||
== Why is it saturating? == | == Why is it saturating? == | ||
| Line 42: | Line 42: | ||
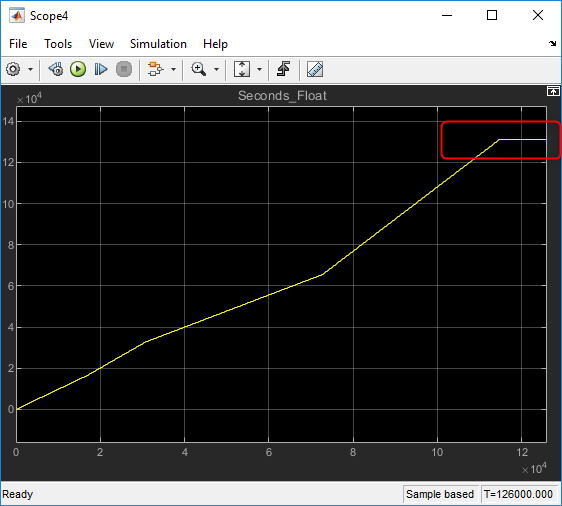
An alternate approach would be to avoid the multiply and division. This will delay the saturation, but the floating point round off will still occur with the addition operation: | An alternate approach would be to avoid the multiply and division. This will delay the saturation, but the floating point round off will still occur with the addition operation: | ||
[ | [[File:Saturation_float_accumulate_36hours.png]] | ||
You will also notice that the slope of the accumulation changes over time. This is due to the rounding that occurs on each operation. | You will also notice that the slope of the accumulation changes over time. This is due to the rounding that occurs on each operation. | ||
| Line 48: | Line 48: | ||
A better solution for this algorithm is to use fixed point. Fixed point has a number of desirable properties: | A better solution for this algorithm is to use fixed point. Fixed point has a number of desirable properties: | ||
# It's decimal point location doesn't change and is thus more predictable over a wider range of values | |||
# Less CPU intensive | |||
This model has two solutions: | This model has two solutions: | ||
| Line 89: | Line 89: | ||
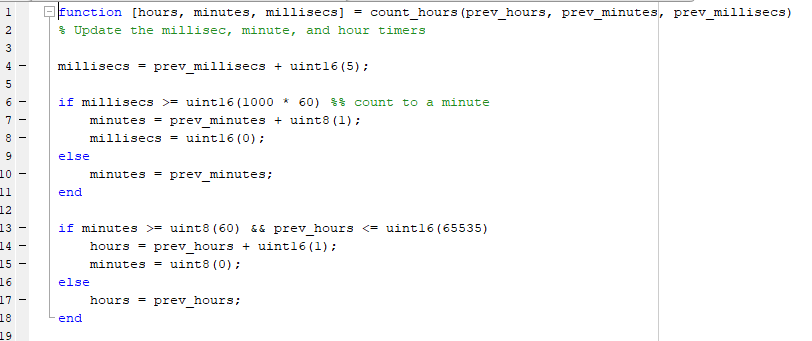
[[File:Fproundoff example mlfunc accumulator code.png]] | [[File:Fproundoff example mlfunc accumulator code.png]] | ||
== | == Solution Comparison using Simulation == | ||
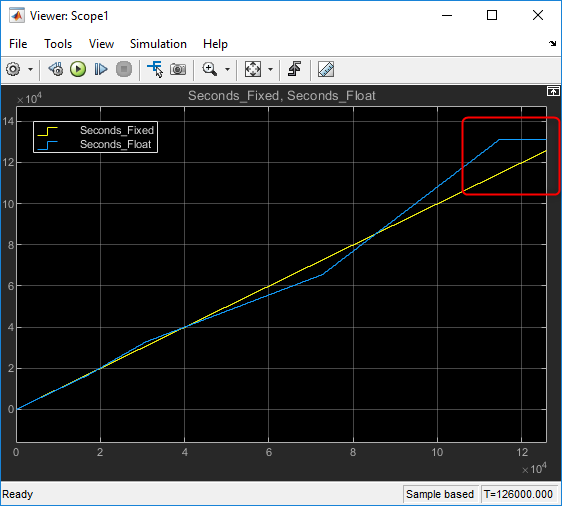
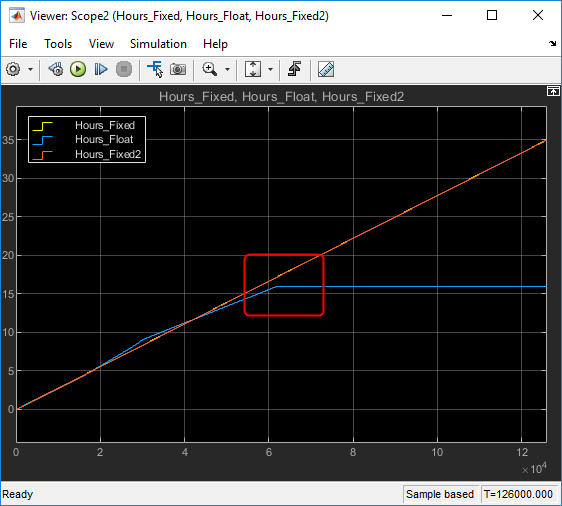
So, how do these solutions compare? | So, how do these solutions compare? Let's simulate: | ||
[ | [[File:Fproundoff seconds fixedvsfloat.png]] | ||
[ | |||
[[File:Fproundoff_hours_accumulator_fixedvfloat.png]] | |||
The fixed point solution offers a more accurate result over the floating point in this particular case and also will saturate at a later time. | The fixed point solution offers a more accurate result over the floating point in this particular case and also will saturate at a later time. | ||
== How do you solve this in Raptor? == | == How do you solve this in Raptor? == | ||
| Line 113: | Line 114: | ||
[[File:Fproundoff example mlfunc accumulator.png]] | [[File:Fproundoff example mlfunc accumulator.png]] | ||
== Inherited Data Type Precision Issue == | |||
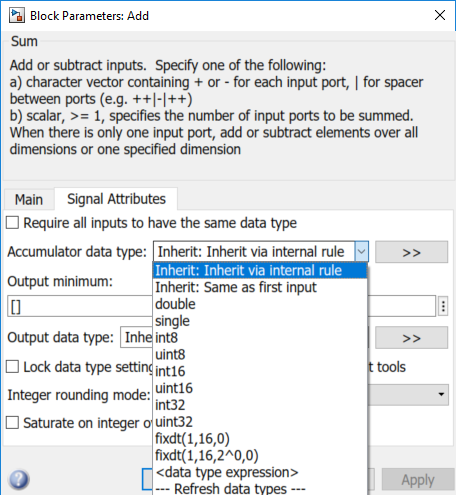
Setting the '''Accumulator data type''' to '''Inherit: Inherit via internal rule''' in the '''Signal Attributes''' tab may cause unexpected behavior. | |||
[[File:inheritSupportIssue.png]] | |||
The '''Inherit''' option may default to a ''single'' data type, depending on the data types of the ports and the chosen target properties. This can lead to the same issues described above, but it will be hidden from view. | |||
Latest revision as of 21:36, 18 January 2019
Floating Point Round Off Error
Recently a Raptor customer had a question about a signal that was saturating and they didn't know why.
The root cause was diagnosed as Floating Point Round Off Error. You can find background information on this phenomenon on Wikipedia. Please look at the link before continuing.
What is an example of floating point round off error? How does it work?
The customer was attempting to create an hour accumulator that would update during a 5 ms task. The customer wanted to view the value in hours in Raptor-Cal. This is a simplified version of their subsystem:
To investigate, simulation is easier to use than running on the controller. The simulation results shows the saturation at 16 hours that the customer claimed:
Why is it saturating?
The hour accumulator saturates due to floating point round off error. The division operation returns the same result despite the addition of .005 to the previous result. As an experiment, MATLAB can illustrate this concept:
>> res = single(16)
res =
single
16.0000
>> res = (single(res)*single(3600)+single(.005))/single(3600)
res =
single
16.0000
That isn't the desired result. The 16 hour saturation limit was much smaller than the design required.
Some different approaches
An alternate approach would be to avoid the multiply and division. This will delay the saturation, but the floating point round off will still occur with the addition operation:
You will also notice that the slope of the accumulation changes over time. This is due to the rounding that occurs on each operation.
A better solution for this algorithm is to use fixed point. Fixed point has a number of desirable properties:
- It's decimal point location doesn't change and is thus more predictable over a wider range of values
- Less CPU intensive
This model has two solutions:
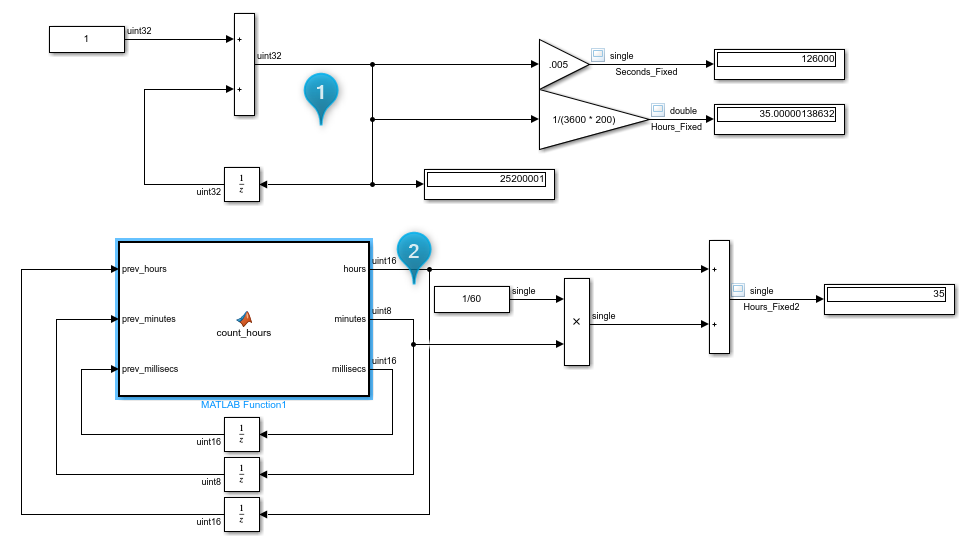
The first implementation uses a 32 bit counter where each tick of the counter represents an increment of 5 ms. However, it will saturate at 249 days:
>> intmax('uint32') / (3600 * 200 * 24)
ans =
uint32
249
This might be acceptable for a particular application. If so, this is the simplest solution.
The second solution is more complex, but it saturates at 7.5 years:
>> 65535/(24 * 365)
ans =
7.4812
The storage type of "hours" could be increased to 32 bits as well, thus increasing the saturation limit to 490K years:
>> intmax('uint32') /(24 * 365)
ans =
uint32
490293
The solution uses a MATLAB Function to implement the time accumulation logic. This is what the logic looks like:
Solution Comparison using Simulation
So, how do these solutions compare? Let's simulate:
The fixed point solution offers a more accurate result over the floating point in this particular case and also will saturate at a later time.
How do you solve this in Raptor?
Now that the basic capability has been verified in simulation, how does this translate to Raptor?
First, all Raptor targets have single precision floating point (not double precision) in the generated code. When determining EPS and other round off considerations, it is important to keep this in mind.
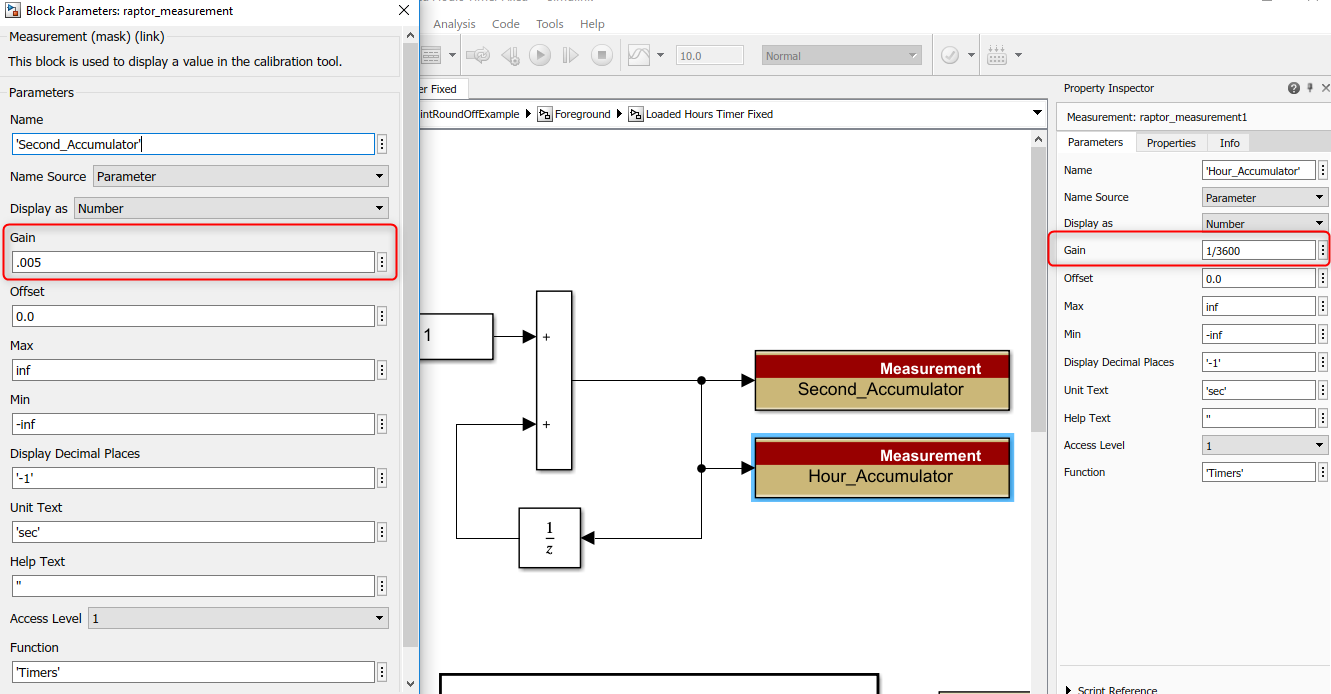
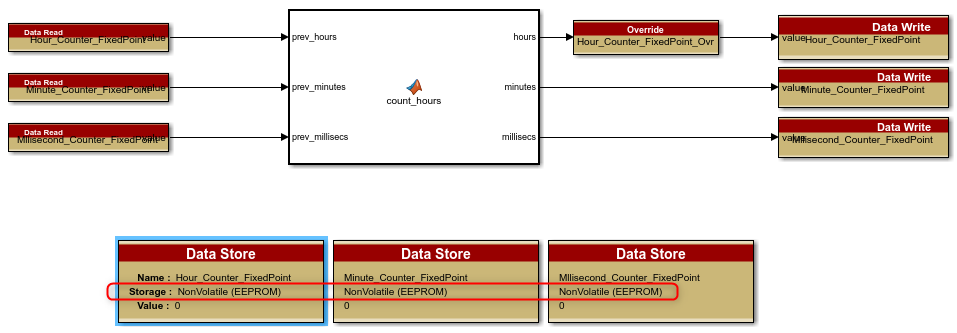
Second, the Simulink generates the code for this logic so Raptor needs to provide the interface to where the memory is stored. It also can use the "Gain/Offset" settings in the Measurement/Data Store blocks to provide the scaling in Raptor Cal or other calibration tools:
The final model might look something like this with NonVolatile data stores and the proper scaling:
Inherited Data Type Precision Issue
Setting the Accumulator data type to Inherit: Inherit via internal rule in the Signal Attributes tab may cause unexpected behavior.
The Inherit option may default to a single data type, depending on the data types of the ports and the chosen target properties. This can lead to the same issues described above, but it will be hidden from view.